La teoría de las catástrofes, o cómo evitar que un perro nos coma crudos

A finales de la década de 1950 René Thom sentó las bases de la Teoría de las Catástrofes. En sus fundamentos explica por qué se desencadenan algunos acontecimientos en forma inesperada, como el caso de un perro que nos parece muy mansito y de pronto se nos abalanza con intenciones homicidas, sin causa aparente.

Lo que nos dice la teoría es que pequeños cambios en el valor de una variable pueden desencadenar grandes cambios en el estado general de un sistema. Por ejemplo, el paso del agua del estado sólido al líquido y al gaseoso. También es aplicable en procesos biológicos, sociales y económicos, así como en los procesos virales de las ideas y modas. Esta capacidad de la teoría de explicar cosas tan disímiles (la cual fue popularizada por los estudios de E. C. Zeeman), fue lo que generó esta especie de "fiebre de las catástrofes". Tanto es así que incluso artistas como Salvador Dalí lo plasmaron en su arte. De hecho, el último cuadro que pintó Dalí ("Cola de golondrina") está basado en la representación gráfica de una de las funciones catastróficas:

Veamos una definición y ejemplo: "Cuando un sistema está en reposo (...) tiende a ocupar un estado estable preferido. Si ese sistema es sometido a las fuerzas del cambio, inicialmente trata de absorber esas fuerzas y a permanecer en su estado estable, pero si las fuerzas son tan fuertes que no puede absorberlas, entonces ocurre un Cambio Catastrófico y se establece un nuevo estado o conjunto de estados de estabilidad. No hay un regreso de continuidad al viejo estado. Imagine una botella sobre una mesa. Está en un estado estable, sin cambios, lo que se llama Equilibrio estable. Ahora imagínese empujando no muy lejos, lentamente, con un dedo, el cuello de la botella. Está ocurriendo un cambio, pero la botella está absorbiendo el cambio de una manera continua. Está en Equilibrio Inestable; si usted deja de hacer presión, la botella volverá a su preferida posición estable. Sin embargo si usted continúa empujando el cuello de la botella, en un momento dado ella caerá. Estará entonces en un nuevo Estado de Equilibrio. Un Cambio Catastrófico ha ocurrido. Un cambio discontinuo ha tenido lugar: una vez que la botella empezó a caer, no hubo un estado estable intermedio disponible hasta que la botella cayó sobre la mesa. (Tomado de coevolucion.net):

En el modelo simplificado, Zeeman toma dos variables que pueden determinar si un perro nos va a atacar o va a salir huyendo: miedo y enojo. Así, generalizando, visualmente podríamos decir que cuanto más miedo tiene un perro, más "aplastadas" estarán sus orejas sobre su cabeza. De la misma manera, se puede decir que estará más enojado cuanto más nos muestre los dientes.

En un modelo tridimensional x, y, z, podríamos graficar un punto en el espacio tomando a x como "cantidad de miedo", a y como "cantidad de enojo" y a z como la consecuencia, o sea, cuál será el comportamiento esperado del perro:

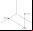
En resumen, se trata de una función que depende de dos variables. El gráfico de los posibles valores que puede tomar crea una superficie en el espacio, con una forma muy particular, que podemos ver en el gráfico siguiente:

Thom demostró, justamente, que el plano es discontinuo. Podemos ver que en la parte media del gráfico la superficie plana se pliega y divide en dos capas superpuestas. Esto indica que, para los valores (x,y) en esa zona, la función puede tomar dos valores; esta es la característica básica del modelo catastrófico. Podemos ver que esto sucede para valores grandes de x e y. En nuestro ejemplo del perro, esta "inestabilidad catastrófica" se produce cuando el animalito tiene simultáneamente altos índices de miedo y enojo. Para darnos una idea, cuando el estado del animal se ubica en esta zona del gráfico, una pequeña modificación en alguna de las variables hará que su estado "salte" sorpresivamente de la capa superior a la inferior, o viceversa, haciendo que el perro "inesperadamente" nos ataque o salga corriendo

Pero hay más: otro factor que incide en la probabilidad de que haya una catástrofe es la forma en que el perro fue juntando cantidades de miedo y enojo. Si empezó con un estado de miedo, es más probable que huya sorpresivamente. En cambio, si en nuestro primer o nos mostró enojo, ¡mucho cuidado! Gráficamente, esto sería equivalente a definir por qué zona del plano el resultado de la función se va "desplazando" a medida que pasa el tiempo.

Les dejamos este videito de ejemplo, todo por el mismo precio:

Hasta aquí, nuestro servicio de hoy orientado a la comunidad propensa a ser masticada por un perro. ¡Vieron qué importante es saber matemáticas!

¡Hasta el próximo To bit!